최근에 새로운 앱 배포 버전에 대한 전환율(특정 행동에 대한 전환/전체 Active User)을 측정해야 할 일이 있었습니다. 아직 배포한 지 며칠 되지 않았기 때문에, 앱 배포 영향에 따른 전환율 변화를 살펴보기 위해 이전 버전과 새로운 버전에 대한 유저들의 전환율을 뽑아보았고, 아래와 같은 결과를 얻었습니다. (데이터는 재현을 위한 가짜 값입니다.)

"흠, 새로운 버전에서 유저들의 전환율이 약 3%p 나 감소했네. 아무래도 UI가 바뀐 것이 익숙하지 않아서 그런걸까?"
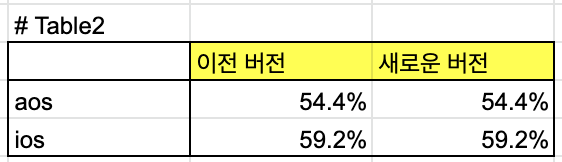
원인을 찾아보기 위해 안드로이드 os와 ios를 각각 살펴보았습니다. (배포하다보면 특정 os나 기기에서 로그 데이터 수집이 제대로 되지 않는 경우는 너무나도 흔하기 때문이지요)
??
그런데 안드로이드와 ios를 구분해서 살펴보았더니 이전 버전과 새로운 버전에서 전환율이 차이가 나지 않는(오차범위 내의) 결과를 보였습니다.
똑같은 표본을 가지고 살펴봤는데, 왜 두 분석에서 전환율 차이에 대한 완전히 다른 결과가 나오는 것일까요?
그 때, 통계학 교과서에서 보았던 '심슨의 역설'이 생각났습니다.
"아, 혹시 이게...?"
심슨의 역설이란?
'심슨의 역설'(Simson’s Paradox)은 1951년에 영국의 통계학자 에드워드 심슨이 설명한 통계적 현상입니다.

심슨의 역설을 한 마디로 설명하자면 '각각의 변수에 신경 쓰지 않고 전체 통계 결과를 유추하다 일어나는 오류' 라고 할 수 있습니다.
『A/B 테스트: 신뢰도 높은 온라인 통제 실험 』 (2020, Ron Kohavi)에서는 심슨의 역설에 대해서 아래와 같이 설명하고 있습니다.
- 통계적 결과에 대한 지표를 비율로 판단할 때, 두 개 이상 그룹의 변형군 사이에서 비율이 서로 다를 경우에 결과를 합쳐서 해석하는 것은 엉뚱한 결론을 내리게 만들 수 있다.
- 예를 들어 실험군과 대조군의 비율이 서로 다른 두 기간이 존재할 때, 첫 번째 단계와 두 번째 단계에서는 실험군이 대조군보다 나을 수 있지만, 두 기간을 합치면 전반적으로 더 나쁠 수 있다.
즉, 위의 문장을 수학식으로 표현하면
$$ a+c/b+d > A+C/B+D $$이면서
$$ a/b < A/B , c/d < C/D $$일 수 있다는 것입니다.
신기한 현상이지만, 숫자를 대입해서 확인해보면 수학적으로는 아무 문제가 없음을 알 수 있습니다.
이러한 현상을 비직관적이라 해서 심슨의 '역설'(Paradox)라고 부릅니다.
그런데, 이런 교과서에 나오는 설명으로는 잘 이해가 되지 않는 것 같기도 합니다. 심슨의 역설의 실제 예를 한 번 살펴볼까요?
심슨의 역설의 예
사실 이러한 심슨의 역설은 백분율 형태의 통계적 결과를 도출해야 하는 분석에서 자주 발견할 수 있는 현상입니다. 처음 직관적으로 살펴본 전체 결과와는 반대되는 역설적인 상황이 발생하는 현상이지요.
쉽게 알아보기 위해 심슨의 역설을 설명하는 나무위키의 예시를 살펴보겠습니다.
심슨대학교에 컴퓨터공학부와 생명과학부 두 과만 있다고 가정하고 전체 합격률을 성별을 나누었을 때, 아래와 같은 결과가 나왔습니다.
| 지원자 | 합격자 | 합격률 | |
| 남학생 | 1000명 | 730명 | 73% |
| 여학생 | 1000명 | 270명 | 27% |
이 결과를 보면 심슨대학교는 남학생의 합격률이 여학생의 합격률보다 월등히 높은 것으로 보입니다.
하지만 '학부'라는 변수를 추가하면 결과는 다르게 나옵니다.
컴퓨터공학부의 합격자 비율 결과를 살펴보면, 아래의 표와 같이 여학생의 합격률이 남학생의 합격률보다 높게 나오고
| 지원자 | 합격자 | 합격률 | |
| 남학생 | 900명 | 720명 | 80% |
| 여학생 | 200명 | 180명 | 90% |
생명과학부 또한 아래의 표와 같이 여학생의 합격률이 남학생의 합격률보다 높다고 나옵니다.
| 지원자 | 합격자 | 합격률 | |
| 남학생 | 100명 | 10명 | 10% |
| 여학생 | 800명 | 90명 | 11.25% |
즉, 전체결과를 보았을 때는 남학생의 합격률이 높은 것으로 나왔지만 세부 학과별로 살펴보면 여학생의 합격률이 더 높은 결과가 나옵니다.
위의 통계적 결과에 대한 결론을 내릴 때, 연구자는 '통계적으로 심슨대학교 지원자 전체의 합격률은 남학생이 높지만, 각 학과별로 살펴보았을 때는 여학생의 합격률이 높다' 라는 결론을 내리는 것이 맞을 것입니다.
여기서 중요한 것은 '연구자가 이 연구의 목표와 연구의 핵심이 되는 변수를 파악해야한다' 라는 것입니다.
사실 위와 같은 결과가 나온 이유는 각 부분의 샘플의 크기와 비율이 다른데도 불구하고 가중치를 주지 않아서 자연스럽게 전체 결과에서는 가중평균이 적용되었기 때문입니다.
예시의 숫자를 살펴보면 두 학부 지원자에서 남녀의 성비가 달랐고, 여학생의 경우 상대적으로 합격률이 낮은 생명과학부에 지원자들이 집중되어 있었기 때문에 전체 합격률이 낮았던 것이지요.
결과적으로, 많은 지원자에 비해 합격률이 낮았던 생명과학부의 합격률(비율) 결과가 전체에서는 큰 가중치를 가지고 영향을 주었던 것입니다!
이렇게 결과에 영향을 주는 핵심 변수를 '혼재변수'(confounding variable or hidden variable) 이라고 합니다. 연구자는 연구의 목적에 따라 누락되는 혼재변수가 없게 통계적 결과를 고려하여 결론을 도출해야 합니다.
위의 결과에 대한 최종 결론은 '각 학과별 합격률을 살펴보았을 때, 학과별 여학생 지원자의 합격률이 남학생보다 높다.' 이 되겠네요!
(지원자들은 각 학부의 지원자들과 경쟁을 하므로, 전체를 보는 것 보다는 부분을 봐야 하니까요.
앱 배포에서 발견한 심슨의 역설 현상
다시 앱 배포 후 전환율에서 발견했던 현상으로 돌아가보겠습니다.
전체 결과에서는 이전 버전과 새로운 버전에서 전환율의 차이를 보였는데, 안드로이드와 ios를 구분해서 살펴보았더니 이전 버전과 새로운 버전에서 전환율이 차이가 나지 않는 현상을 보였습니다.
이 현상에 대해서 위에서 살펴본 '심슨의 역설'의 영향이라고 의심하며 각각 전환율의 구체적인 숫자를 살펴보았습니다.


아! 각 샘플의 숫자까지 자세히 살펴보니 이런 현상이 왜 일어났는지 알 수 있습니다. ios에서 새로운 버전의 샘플 숫자가 훨씬 적었고, 전체 결과로 합산하였을 때, 상대적으로 전환율이 높은 ios의 적은 샘플 숫자가 가중적용된 전형적인 '심슨의 역설' 현상이었습니다. (반대로 말하자면 상대적으로 전환율이 더 나쁜 aos의 영향이 전체 결과에 더 많은 영향을 준 것이지요.)
앱 서비스의 배포에서 이런 현상이 일어난 이유를 정리해보면 아래와 같습니다.
- 앱 서비스는 ios가 aos보다 배포율이 훨씬 느리다 (app store에서 3일의 심사기간을 두기 때문)
- 그렇기 때문에 앱이 배포되는 중에 전환율을 변화를 살펴본다면 반드시 os별로 따로 살펴보아야 한다.
앱 서비스 배포 상황에서는 'os'가 혼재변수였습니다. 정확하게 분석하려면 os라는 혼재변수를 누락하지 않은 상태에서 데이터를 살펴보는 것이 더 정확합니다. 위 경우에 결과를 합쳐서 해석하는 것은 엉뚱한 결론을 내릴 수 있습니다.
결론 : 심슨의 역설을 대응하는 데이터 분석가의 자세
앞에서 살펴본 것처럼 심슨의 역설은 비직관적이지만 드물지 않게 나타납니다.
그렇기에 분석가(연구자)는 다른 비율로 수집된 샘플의 데이터를 합산할 때에 항상 유의해야 합니다!
부분의 결과와 전체의 결과(결과 지표가 비율과 관련된, 그룹 표본의 수에 따라 가중 평균이 적용될 수 있는)가 다를 경우에 혼재변수가 누락되어 전체의 결과가 나온 것은 아닌지 살펴보는 습관을 가져야겠습니다.
결론적으로 분석가는 분석의 목적에 따라 어떤 데이터(모집단 혹은 하위 모집단)를 사용할지를 결정하고, 필수적인 변수를 고려하여 올바른 결론을 내려야 합니다.
심슨의 역설을 기억하며, 통계에게 속지 않기를!
참고문헌
Ron Kohavi, Diane Tang & Ya Xu, 『A/B 테스트: 신뢰도 높은 온라인 통제 실험』, 에이콘출판사, 2022
"심슨의 역설", 나무위키, 2022년9월3일 수정, 2022년11월12일 접속, https://namu.wiki/w/심슨의%20역설
* 항상 배우는 중입니다! 위의 글에서 잘못된 내용을 발견하셨다면 댓글 달아주시면 정말 감사하겠습니다 :)
'Data Science' 카테고리의 다른 글
| 데이터 분석가가 가져야할 ‘인사이트’ (0) | 2023.03.15 |
|---|---|
| 데이터 분석가는 어떤 일을 하는가 (0) | 2023.01.19 |

